Quantum Tic-Tac-Toe
How to play quantum tic-tac-toe
This tic-tac-toe game is based on three phenomena in quantum mechanics (explained below).
Link to Wikipedia article
Terminology
State A state is a condition which a square can be in. The two possible states are X and O, which are the marks used in this game. We differenciate between two kinds of states in this game.
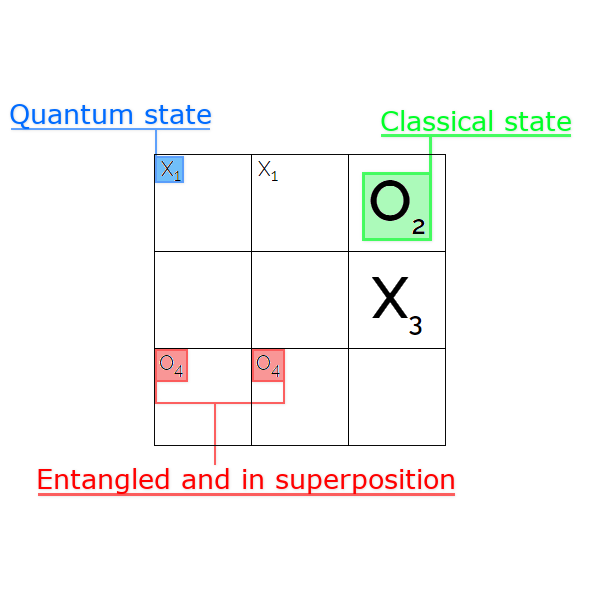
Quantum state: A quantum state are the marks we first place, and we will always place two quantum states, which will be in superposition and become entangled. The subscript number associated with the quantum state can tell us which other state it is connected to.
Classical state: A classical state is what we would consider a normal mark in the classic version of tic-tac-toe. The classical states are written with a large mark. All classical states in this game have been quantum states before, but have collapsed since.
This version is based on these three phenomena:
Superposition: This phenomenon means that a state can be in two states at the same time. In this game that means that a state can be in two squares at the same time, which is why we can place the same mark in two places. Therefore two quantum states with the same mark and number means that they are in superposition, and in principle are the same mark. In the image the two X1 are in superposition, because they have equal states and are in two different squares. The same applies to the two O4.
Entanglement: This phenomenon describes a connection between two objects. In this game that means that two identical marks share a correlation, and when one of the marks collapses, the other entangled mark will also collapse. In the image the two X1 are entangled. The same applies to the two O4. In this game every superposition are also entangled with the corresponding state.
Collapse: This phenomenon causes quantum states to reduce to classical states. A collapse occurs when a measurement takes place. In this game that means that when a cycle is detected, the player which did not place the last mark will need to make a measurement, and therefore collapse the states. All the quantum states which are entangled with the collapsed square will also collapse into a classical state, and cause a chain reaction.
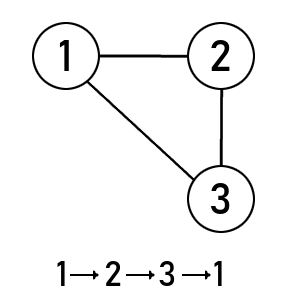
Cycle: A cycle is a closed path where the path starts and ends with the same square. We can see if a there is a cycle by going through the entanglements and seeing if the square we started with is the same as the one we end with. In the image to the right, we can see an example of a cycle. The cycle is created with the entanglements which connect the squares and create a closed path. We can trace the path by going through the entanglements, so let's start with square 1, where X1 is entangled with square 2. O2 connects square 2 and 3. Then X3 connects square 3 and 1. Now the path starts and ends with square 1, and therefore creates a cycle of entanglements. This can be visualized with a graph, which is shown in the image below the tic-tac-toe grid.
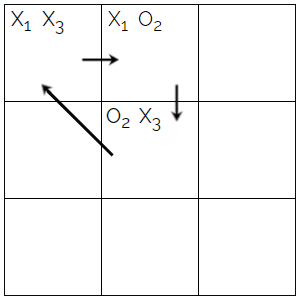
Gameplay
First select the size of the grid of your choosing, then press Start.
You will be greeted with a grid with dimensions based on the size you selected. This explanation will be based on a 3x3 grid, but the rules stay the same for any sized grid.
X always starts, and on each move the current player marks two squares with their letter (instead of just one, like in the classical tic-tac-toe). Each letter is subscripted with the number of the move.
The players place marks until either one win or it ends in a draw.
Collapse:
If the quantum states form a cycle (cyclic entanglement), then it is the player whose turn it's not (that is, the player who didn't create the cycle), chooses which of the two possible states the last play collapses into.
This will result in the rests of the states that also are in the cycle to collapse into a classical state.
When a move collapses into a single square, that square becomes permanently marked (with a larger letter), and it has become a classical state. A collapse will affect all other squares that are entangled, and cause a chain reaction.
How to win
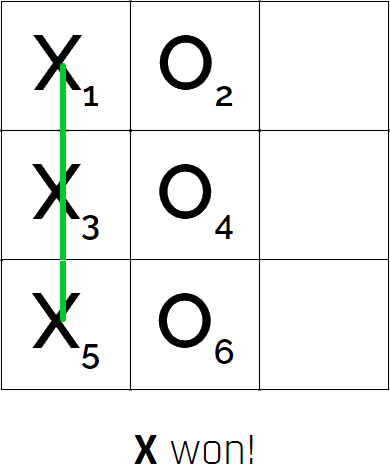
A player wins by getting a full row (or collumn or diagonal) of classical states. This means that you win the same way as regular tic-tac-toe, but you cannot win with the quantum states, only the classical. However it's possible that a measurement causes the entire board to collapse and give both a full row. To determine the winner we need to look at the small number assigned with each classical state. Then we find the largest number in each winning row, and compare them. The row with the lowest of these numbers is the winning row. We can see an example of this on the image to the right. If we find the largest number in each row, we find that the X's largest number is 5 and the O's largest number is 6. Since 5 is smaller than 6, X wins the round.